שלשה פיתגורית

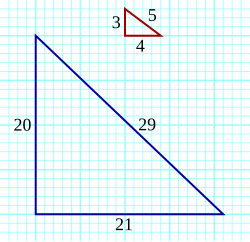
שלשה פיתגורית (או שלשה פיתגוראית) היא שלשה של מספרים טבעיים המקיימת את השוויון $a^{2}+b^{2}=c^{2}$ , המופיע במשפט פיתגורס. בהתאם למשפט ההפוך למשפט פיתגורס, משולש שצלעותיו מהוות שלשה פיתגורית הוא משולש ישר-זווית. השלשה הפיתגורית הקטנה ביותר, $(3,4,5)$ , הייתה ידועה משחר ההיסטוריה, ומשערים שהמשולש ישר הזווית שמתקבל ממנה שימש להעברת אמות מים עוד במצרים הקדומה.

כל שלשה פיתגורית אפשר להכפיל בגורם קבוע שלם, ולקבל שלשה פיתגורית חדשה (אם $(a,b,c)$ היא שלשה פיתגורית, אזי $a^{2}+b^{2}=c^{2}$ ולכן גם $(ak)^{2}+(bk)^{2}=(ck)^{2}$ , כאשר $(ak,bk,ck)$ גם היא שלשה פיתגורית). שלשה פיתגורית שלא ניתן לקבל כמכפלה של שלשה פיתגורית אחרת בקבוע שלם גדול מ-1 נקראת שלשה פרימיטיבית: אלו הן השלשות $(a,b,c)$ שבהן המחלק המשותף המקסימלי הוא 1; בשלשה כזו, המחלק המשותף המקסימלי של כל שני מספרים הוא 1.

להלן רשימת 16 השלשות הפרימיטיביות שבהן $c\leq 100$ :

(3,4,5)	(5,12,13)	(15,8,17)	(7,24,25)
(21,20,29)	(35,12,37)	(9,40,41)	(45,28,53)
(11,60,61)	(33,56,65)	(63,16,65)	(55,48,73)
(13,84,85)	(77,36,85)	(39,80,89)	(65,72,97)

פרמטריזציה של התבנית הריבועית[עריכת קוד מקור | עריכה]

אפשר לייצר אינסוף שלשות פיתגוריות באמצעות הנוסחה

{\begin{aligned}a&=m^{2}-n^{2}\\b&=2mn\\c&=m^{2}+n^{2}\end{aligned}}

כאשר $m,n$ מספרים טבעיים. ההוכחה שאלו אכן שלשות פיתגוריות היא על ידי חישוב ישיר:

(m^{2}-n^{2})^{2}+(2mn)^{2}=m^{4}+2m^{2}n^{2}+n^{4}=(m^{2}+n^{2})^{2}

משערים שנוסחה זו הייתה ידועה כבר לבבלים, שיצרו לוח בכתב יתדות (לוח פלימפטון 322) המתוארך לתקופה שבין שנת 1900 לפנה"ס לשנת 1600 לפנה"ס וכולל חמש-עשרה שלשות פיתגוריות, ובהן $1771^{2}+2700^{2}=3229^{2}$ (אותה אפשר לקבל אם נבחר $m=50,n=27$ ).

בפרט, אם נציב $m=n+1$ נקבל את השלשות

{\begin{aligned}a&=2n+1\\b&=2n(n+1)={\frac {a^{2}-1}{2}}\\c&=2n^{2}+2n+1={\frac {a^{2}+1}{2}}\end{aligned}}

לכן כל מספר אי-זוגי (למעט המספר $1$ ) הוא חלק משלשה פיתגורית פרימיטיבית, ומכאן שיש אינסוף שלשות פיתגוריות פרימיטיביות.

משפט: כל שלשה פיתגורית פרימיטיבית אפשר להציג באמצעות הנוסחה שבראש הסעיף, כאשר $m,n$ זרים ובעלי זוגיות שונה.

הוכחה: נבחין שאם $(a,b,c)$ שלשה פרימיטיבית, אזי $c$ מוכרח להיות אי-זוגי, וכן גם אחד (בדיוק) מבין המספרים $a,b$ (זאת משום שריבוע משאיר תמיד שארית 0 או 1 בחלוקה ל-4). יהי $b$ המספר הזוגי בשלשה. מן השוויון $a^{2}+b^{2}=c^{2}$ נובע $b^{2}=c^{2}-a^{2}=(c-a)(c+a)$ , כאשר $c-a,c+a$ שניהם זוגיים. מכיוון ש- $a,c$ זרים מתקיים כי $\gcd {\bigl \{}c-a,c+a{\bigr \}}=2$ , ומכיוון שמכפלתם היא $b^{2}$ נובע כי כל אחד מן הגורמים הוא פעמיים ריבוע. אם נכתוב $c-a=2s^{2},c+a=2t^{2}$ נקבל את ההצגה הדרושה. כעת $s,t$ זרים משום שכל מחלק משותף שלהם מחלק גם את $a,b,c$ , ואחד מהם זוגי משום שאחרת $a,b,c$ כולם זוגיים.

מכאן אפשר לקבל נוסחה כללית לכל השלשות הפיתגוריות:

{\begin{aligned}a&=(m^{2}-n^{2})k\\b&=2mnk\\c&=(m^{2}+n^{2})k\end{aligned}}

כאשר $m,n$ זרים ובעלי זוגיות שונה; כל שלשה מוצגת כך באופן יחיד (משום ש- $k$ הוא המחלק המשותף המקסימלי של שלושת המספרים). זוהי דוגמה לפתרון של משוואה המתקבלת מתבנית ריבועית עם נקודה רציונלית. ישנן שלשות, כגון $(9,12,15)$ , שלא ניתן להציג עם $k=1$ (במקרה זה, משום ש-15 אינו סכום של שני ריבועים).

על ידי בחינת הערכים האפשריים של $m,n$ מודולו מספר קבוע $k$ , אפשר להסיק אלה שאריות יכולה לקבל שלשה פרימיטיבית בחלוקה ל- $k$ . לדוגמה, אחד מבין המספרים $a,b$ מתחלק ב-4 והשני אי-זוגי; גם $c$ אי-זוגי; בפרט, מספר הנותן שארית 2 בחלוקה ל-4 אינו יכול להופיע בשלשה פיתגורית פרימיטיבית. בדומה לזה, בדיוק אחד משני המספרים $a,b$ מתחלק ב-3, ובדיוק אחד מבין השלושה מתחלק ב-5.

מאחר ש- $c$ הוא סכום של שני ריבועים (זרים זה לזה), כל גורם ראשוני שלו הוא מהצורה $4k+1$ .

כל מספר טבעי שאינו נותן שארית 2 בחלוקה ל-4 יכול להופיע בתפקיד $b$ בשלשה פרימיטיבית. מספר השלשות הפרימיטיביות (עם $a>0$ ) שבהן $b$ מופיע שווה ל- $2^{s-1}$ , כאשר $s$ הוא מספר הגורמים הראשוניים השונים של $b$ .

כאשר $m,n$ בנוסחה שבראש פרק זה הם מספרי פל עוקבים, ההפרש בין $a,b$ בשלשה המתקבלת הוא 1.^[1]

העץ הטרנארי של השלשות הפיתגוריות[עריכת קוד מקור | עריכה]

אם $(a,b,c)$ שלשה פיתגורית, אזי המספרים

{\begin{aligned}n_{1}&=c-b\\n_{2}&=c-a\\n_{3}&=a+b-c\end{aligned}}

מקיימים את היחס $n_{3}^{2}=2n_{1}n_{2}$ ; ולהפך, אם $(n_{1},n_{2},n_{3})$ מקיימים את היחס הזה, ניתן לבנות מהם שלשה פיתגורית באמצעות הטרנספורמציה ההפוכה:

{\begin{aligned}a&=n_{1}+n_{3}\\b&=n_{2}+n_{3}\\c&=n_{1}+n_{2}+n_{3}\end{aligned}}

במילים אחרות, אם מגדירים

T(a,b,c)=(c-b,c-a,a+b-c)

אזי $T$ מעבירה את היריעה ${\bigl \{}(a,b,c):a^{2}+b^{2}=c^{2}{\bigr \}}$ ליריעה ${\bigl \{}(n_{1},n_{2},n_{3}):n_{3}^{2}=2n_{1}n_{2}{\bigr \}}$ .

היתרון הוא, כמובן, שאת המשוואה השנייה קל יותר לפתור (במספרים שלמים). השלשה $(a,b,c)$ פרימיטיבית אם ורק אם $n_{1},n_{2}$ זרים.

משפט רוברטס[עריכת קוד מקור | עריכה]

משפט: הווקטור $(a\,\,b\,\,c)$ מהווה שלשה פרימיטיבית אם ורק אם $(a\,\,b\,\,c)=M\cdot (3\,\,4\,\,5)$ , כאשר $M$ מכפלת מספר סופי של מטריצות מבין:

T_{1}={\begin{bmatrix}1&2&2\\-2&-1&-2\\2&2&3\end{bmatrix}},\quad T_{2}={\begin{bmatrix}-1&-2&-2\\2&1&2\\2&2&3\end{bmatrix}},\quad T_{3}={\begin{bmatrix}1&2&2\\2&1&2\\2&2&3\end{bmatrix}}

יצוג השלשות כעץ טרנארי: בדרך זו, ניתן להציג את כל השלשות הפרימיטיביות בעץ טרנארי, עץ שבו לכל קודקוד יש בדיוק שלושה בנים. שורש העץ יהיה השלשה $(a\,\,b\,\,c)$ . לכל שלשה $P=(a\,\,b\,\,c)$ יהיו שלושה בנים:

P_{1}=P\cdot T_{1},\quad P_{2}=P\cdot T_{2},\quad P_{3}=P\cdot T_{3}

רעיון ההוכחה: לכל שלושה מספרים טבעיים המהווים שלשה פיתגורית $P=(a\,\,b\,\,c)$ נגדיר את השלשות המסומנות המתקבלות ממנה:

P_{1}=(-a\,\,b\,\,c),\quad P_{2}=(a\,\,-b\,\,c),\quad P_{3}=(-a\,\,-b\,\,c)

נגדיר את ה'תאום' של שלשה המתאימה ל- $(n_{1},n_{2},n_{3})$ השלשה המתקבלת מהחלפת $n_{3}$ ב- $-n_{3}$ . יהיו $P_{1}',P_{2}',P_{3}'$ תאומי $n_{1},n_{2},n_{3}$ של $P_{1},P_{2},P_{3}$ בהתאמה. מניתוח התהליך ניתן להסיק כי $P_{1}',P_{2}',P_{3}'$ הן שלשות פיתגוריות של מספרים טבעיים וכי לכל $i=1,2,3$ מתקיים $P_{i}'=P\cdot T_{i}$ . כדי להוכיח את הכיוון ההפוך מוצאים לכל שלשה פיתגורית (לא מסומנת) $P=(a\,\,b\,\,c)$ את התאום שלה $P'=(a'\,\,b'\,\,c')$ ומבצעים תהליך דומה.

שלשות פיתגוריות מיוחדות[עריכת קוד מקור | עריכה]

פייר דה פרמה מצא שלשה פיתגורית $(a,b,c)$ כאשר $a+b,c$ ניתנים להצגה כריבוע של מספר טבעי:

{\begin{aligned}a&=4565486027761\\b&=1061652293520\\a+b&=2372159^{2}\\c&=2165017^{2}\end{aligned}}

בנוסף, פרמה הוכיח בנסיגה אינסופית כי לא יתכנו שלשות פיתגוריות בהן

a,b

הם ריבועים של מספרים שלמים.

קיימות שלשות פיתגוריות שונות עם אותו ערך של המכפלה $ab$ . למשל, בשלשות

(70,24,74),(42,40,58),(15,112,113)

מתקיים

ab=1680

. לא ידוע האם קיימות שלשות עבורן

abc

זהה.

קיימות אינסוף שלשות פיתגוריות שבהן $a,b$ הם מספרים עוקבים. ארבע השלשות הראשונות מסוג זה הן

(3,4,5),(20,21,29),(119,120,169),(696,697,985)

מאחר ש-

c

הוא סכום של שני ריבועים עוקבים, המשוואה המתאימה לכך היא

a^{2}+(a+1)^{2}=c^{2}

, כלומר

2a^{2}+2a+1=c^{2}

. לאחר הכפלה ב-2 והעברת אגפים תתקבל המשוואה

(2a+1)^{2}-2c^{2}=-1

. זוהי משוואת פל שפתרונותיה ידועים. לאחר הוספת הביטוי

2c^{2}

לשני האגפים והוצאת שורש ריבועי, מתקבלת האפשרות לבודד את

a

ולהגיע למשוואה

a={\frac {{\sqrt {2c^{2}-1}}-1}{2}}

. מכאן ניתן לגלות את הנוסחאות הכלליות ל-

a,b,c

בשלשות פיתגוריות שבהן

a,b

עוקבים:

{\begin{aligned}a_{n}&={\frac {(1+{\sqrt {2}})^{2n+1}+(1-{\sqrt {2}})^{2n+1}-2}{4}}\\b_{n}&={\frac {(1+{\sqrt {2}})^{2n+1}+(1-{\sqrt {2}})^{2n+1}+2}{4}}\\c_{n}&={\frac {(1+{\sqrt {2}})^{2n+1}-(1-{\sqrt {2}})^{2n+1}}{2{\sqrt {2}}}}\end{aligned}}

הכללות[עריכת קוד מקור | עריכה]

הכללה מפורסמת של בעיה זו היא המשפט האחרון של פרמה הקובע שאין פתרון במספרים טבעיים למשוואה $\ a^{n}+b^{n}=c^{n}$ עבור חזקות הגדולות מ-2.
משוואת לז'נדר: לאלה מספרים טבעיים $u,v,w$ יש פתרון במספרים טבעיים למשוואה $ux^{2}+vy^{2}=wz^{2}$ ? עבור $u=v=w$ הפתרונות הם כמובן שלשות פיתגוריות.